Mô hình hóa biến dạng góc trong quá trình ép liên tục bằng ma sát bề mặt qua kênh gấp khúc...
06/12/2017
Trong báo cáo cũng đã đưa ra sự phân bố và biến thiên tốc độ biến dạng, sự chênh lệch biến dạng giữa đỉnh và đáy mẫu để đánh giá mức độ đồng đều trong kỹ thuật CFAE.
Mô hình hóa biến dạng góc trong quá trình ép liên tục bằng ma sát bề mặt qua kênh gấp khúc có tiết diện không đổi (CFAE) bằng phương pháp phần tử hữu hạn (FEM)
Modeling shear deformation during continuous priftional angular pressing by finite element method
Phạm Quang, Đào Minh Ngừng và Đỗ Minh Nghiệp Khoa Khoa học và công nghệ vật liệu Trường ĐHBK Hà Nội, Số 1 Đại Cồ Việt Hà Nội
Tóm tắt
Đề tài sử dụng phần mềm DEFORMTM 2D trên cơ sở thuật toán phần tử hữu hạn (Finite Element Method, FEM) để mô phỏng số quá trình ép liên tục bằng ma sát bề mặt trong kênh gấp khúc tiết diện không đổi (Continuous Frictional Angular Pressing, CFAE) nhằm tạo cấu trúc siêu mịn cho vật liệu nhớ hình hệ Ti-Ni. Kết quả mô phỏng đã cho biết độ lớn của góc nghiêng trên mô hình phân tố biến dạng là 56° (phần đỉnh mẫu) và 32° (phần đáy mẫu) sau một lần ép. Trong báo cáo cũng đã đưa ra sự phân bố và biến thiên tốc độ biến dạng, sự chênh lệch biến dạng giữa đỉnh và đáy mẫu để đánh giá mức độ đồng đều trong kỹ thuật CFAE.
Từ khóa: SPD, ECAP, C2S2, CFAE, FEM, UFG, Nitinol, TiNi.
Abstract
The DEFORM TM 2D commercial software package using finite element method (FEM) to simulate te continuous frictional angular pressing (CFAP) process was applied to bulk ultra - fine grained (UFG) Nitinol alloy system (Ji-Ni). The silation refults indicated the shear strain angles on the modeling deformation element at top (56°) and bottom (32°) of work piece. This report also discussed the distribution and evolution of effective strain rate, the strain difference in the cross section of work piece during CFAP process.
1. Mở đầu
Sự thay đổi tổ chức hạt của vật liệu kim loại trong quá trình biến dạng dẻo được nghiên cứu rộng rãi từ vài thập kỷ trước [1-2]. Đã khẳng định rằng biến dạng ở trạng thái nguội làm cho kích thước hạt trung bình của vật liệu kim loại giảm xuống đáng kể. Do đó, phương pháp biến dạng dẻo mãnh liệt (Severe Plastic Deformation, SPD) được phát triển từ những năm 1970 bởi các nhà khoa học Nga là một trong những phương pháp hữu hiệu để tạo ra vật liệu khối có cỡ hạt siêu mịn (Ultrafine Grained, UFG).
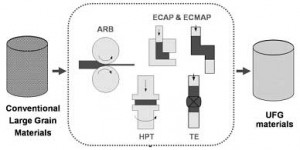
Hình 1. Sơ đồ một số phương pháp SPD
Phương pháp biến dạng dẻo mãnh liệt được định nghĩa là quá trình tạo hình kim loại với mức độ biến dạng rất lớn, áp đặt lên vật rắn dạng khối và có thể làm nhỏ hạt trong quá trình gia công. Kích thước hạt của vật liệu sau khi được chế tạo bằng phương pháp này thông thường nhỏ hơn 1 μm, tuỳ thuộc vào việc sử dụng kỹ thuật nào của SPD (hình 1). Các kỹ thuật này khá đa dạng, ví dụ: kỹ thuật ép trong kênh gấp khúc tiết diện không đổi (Equal Channel Angular Pressing, ECAP) [3-6], kỹ thuật xoắn dưới áp lực cao (High-Pressure Torsion, HPT) [7], kỹ thuật cán dính tích luỹ (Accumulative Roll-Bonding, ARB) [8], kỹ thuật rèn đa chiều (Multi-Directional Forging, MDF) [9], (equal channel multi-angular pressing, ECMAP) [10], kỹ thuật ép đùn xoắn (Twist Extrusion, TE) [11], v.v... đã được phát triển để chế tạo vật liệu khối siêu mịn.
1.1. Kỹ thuật ECAP và CFAE
Trong các phương pháp SPD, kỹ thuật ECAP là phương pháp phổ biến và có nhiều ưu việt. Nguyên lý biến dạng của kỹ thuật ECAP dựa vào cơ chế trượt của biến dạng dẻo, quá trình cắt, trượt đơn này xảy ra trên đường giao giữa hai kênh. Kỹ thuật ECAP có nhiều ưu điểm nổi bật như: (i) biến dạng lớn đạt được bằng cách lặp lại quá trình ép mà không thay đổi hình dạng phôi ban đầu và được phân bố đều trên toàn bộ tiết diện, (ii) Cấu trúc nhận được là đồng nhất, không có hiện tượng rỗ xốp, (iii) có thể áp dụng với nhiều loại vật liệu cấu trúc khác nhau (kim loại, hợp kim biến cứng phân tán, liên kim, composite,...) [12-15] với hình dạng phôi đủ lớn khác nhau và cuối cùng là (iv) với yêu cầu lực ép gia công thấp.
Kỹ thuật ECAP sử dụng khuôn có thiết kế với hai thông số hình học đặc trưng là góc kênh Φ và góc lượn ψ [16]:
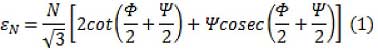
trong đó góc kênh (Φ) là góc giao nhau giữa hai kênh và góc lượn (ψ) là góc biểu thị phần cung ngoài nối giữa hai rãnh giao nhau của kênh kép trong khuôn. Trong quá trình ECAP, phôi có thể được ép nhiều lần, trong trường hợp ép vật liệu khó biến dạng, quá trình ECAP được điều chỉnh ở nhiệt độ thích hợp để quá trình biến dạng của phôi được dễ dàng hơn. Trong vài năm trở lại đây, trường Đại học Bách khoa Hà Nội đã nghiên cứu các đề tài về kỹ thuật ECAP để chế tạo vật liệu có cấu trúc siêu mịn (Ti và Al) trong chương trình hợp tác nghiên cứu quốc tế giữa TTNC Vật liệu học với Viện KIMS của Hàn Quốc (Korea Institute of Materials Science) và đã có những kết quả công bố trên các tạp chí khoa học trong nước và quốc tế [19].
Tuy nhiên do hạn chế về kích thước mẫu, thao tác thủ công không liên tục nên chỉ thích hợp phục vụ nghiên cứu trong phòng thí nghiệm. Một kỹ thuật mới ra đời nhằm đáp ứng được quy mô sản xuất lớn, ứng dụng trong công nghiệp đó là kỹ thuật ép liên tục trên bề mặt (Continuous Confined Strip Shearing, C2S2) [20]. Kỹ thuật này là sự kết hợp của ECAP với biện pháp ép liên tục bằng các phương pháp khác nhau, do đó khắc phục được hạn chế về kích thước và chiều dài của mẫu dùng trong kỹ thuật ECAP. Quá trình thực hiện bằng cách phối hợp rất nhiều quy trình lại với nhau như ép trong kênh không đồng dạng (Dissimilar Channel Angular Pressing, DCAP) [21], cán trong kênh tiết diện không đổi (Equal Channel Angular Rolling, ECAR) [22].
Ngoài ra, kỹ thuật đùn ép liên tục bằng ma sát bề mặt (Continuous Frictional Angular Pressing, CFAE) [23] đã và đang được phát triển nhằm tạo ra vật liệu cấu trúc siêu mịn với hiệu suất cao. Kỹ thuật CFAE là sự kết hợp của ECAP với quá trình đùn ép liên tục vật liệu bằng cách sử dụng ma sát của trục cán qua lực ép lên bề mặt mẫu là đối tượng nghiên cứu trong báo cáo này.
Đề tài sử dụng phần mềm DEFORMTM 2D trên cơ sở thuật toán phần tử hữu hạn (Finite Element Method, FEM) để mô phỏng số quá trình ép liên tục bằng ma sát bề mặt trong kênh gấp khúc tiết diện không đổi (CFAE) nhằm tạo cấu trúc siêu mịn cho vật liệu nhớ hình hệ Ti-Ni. Bước đầu nghiên cứu thiết lập mô hình công nghệ ép hợp kim Nitinol bằng phương pháp CFAE tại nhiệt độ 25°C. Mô hình hóa phân tố biến dạng và cấu trúc để thấy được quá trình trượt của các mặt tinh thể thông qua góc nghiêng biến dạng cũng như cơ chế làm giảm kích thước hạt khi mẫu qua góc kênh.
Trong nghiên cứu cũng sẽ đưa ra sự phân bố và biến thiên tốc độ biến dạng và sự chênh lệch biến dạng giữa đỉnh và đáy mẫu để đánh giá mức độ đồng đều trong kỹ thuật CFAE.
1.2. Phương pháp phần tử hữu hạn và phần mềm DEFORMTM 2D
Cơ sở tính toán của phương pháp phần tử hữu hạn (Finite Element Method, FEM) là sử dụng điểm (nút) chia lưới xác định, chúng được cố định trên vật thể phân tích. Các phần tử của vật liệu được tạo thành bằng cách kết nối các điểm chia lưới lại với nhau, tập hợp của các phần tử tạo ra một mạng lưới. Khi vật thể biến dạng, điểm chia lưới chuyển động cùng vật thể và các phần tử bị biến dạng, Bởi vậy phương pháp phần tử hữu hạn được tính toán theo chuyển động của các phần tử có thể tích không đổi.
Do các phần tử biến dạng mãnh liệt, nên việc sử dụng thuật toán phần tử hữu hạn trong mô phỏng tạo hình sẽ dẫn đến sự cần thiết phải chia lại lưới (remeshing) các phần tử theo biến dạng toàn bộ của vật liệu. Điều này làm giảm nghiệm của bài toán và làm tăng thời gian xử lý của máy tính. DEFORMTM [24] là phần mềm mô phỏng các quá trình gia công cơ, nhiệt dựa trên phương pháp phần tử hữu hạn (FEM. Chương trình cho phép nhập mô hình hình học của các vật thể trực tiếp hoặc dưới dạng file có đuôi ISG (với 2D) và STL (khối đặc, 3D), một loại file tạo bởi các chương trình thiết kế đồ họa như Solidworks hoặc AutoCAD. Ngoài ra phần mềm này cũng có thể nhập mô hình tính toán dưới dạng dữ liệu từ các phần mềm thiết kế và chia lưới chuyên dụng tương thích khác như Gambit, Patran…
2. Mô phỏng số quá trình CFAE
2.1. Thông số hình học
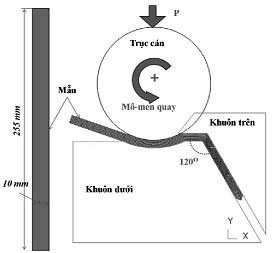
Mô hình hình học (hình 2) trong bài toán mô phỏng được thiết kế trên giao diện của chương trình gồm các thông số hình học sau: (i) Mẫu là thanh dài có kích thước (255 x 10) mm, được chia lưới vuông với 2000 phần tử với mô hình vật liệu biến dạng dẻo. (ii) Khuôn gồm khuôn trên và khuôn dưới với mô hình vật liệu tuyệt đối cứng tạo thành kênh vào và kênh ra của kỹ thuật ECAP với tiết diện không đổi = 10 mm. Góc kênh chính Φ = 120°, góc lượn ψ = 0°. (iii) Trục cán có bán kính R = 70 mm với mô hình vật liệu tuyệt đối cứng.
Hình 2. Mô hình công nghệ CFAE trong mô phỏng số
Trong kỹ thuật CFAE, trục cán đóng vai trò quan trọng trong việc đùn ép liên tục vật liệu vào trong kênh ECAP, do đó mẫu không bị hạn chế về chiều dài. Đây là một điểm nhấn khác biệt của trong việc giải quyết bài toán kích thước của mẫu dùng trong kỹ thuật ECAP trước đó. Hành trình của trục cán gồm hai giai đoạn:
+ Giai đoạn 1: giai đoạn tịnh tiến để ép mẫu với tốc độ v = 1 mm/s.
+ Giai đoạn 2: giai đoạn xoay để đẩy mẫu với tốc độ v = 0,10472 rad/s (1 vòng/phút).
Trong quá trình mô phỏng chương trình tự động chia lại lưới (remeshing) và được hoàn thành trong 10 h trên máy tính cá nhân.
2.2. Các thông số vật liệu của mẫu
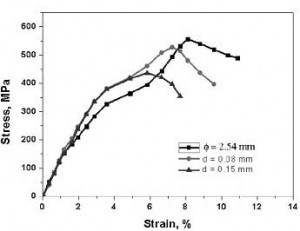
Hình 3. Đồ thị ứng suất - biến dạng của hợp kim Nitinol
Hình 3 là đồ thị đường cong ứng suất-biến dạng của hợp kim Nitinol tại nhiệt độ 25°C với các mẫu có hình dạng và kích thước khác nhau, được trích dẫn trong tài liệu “Smithells Metals Reference” [25]. Trong mô hình này, mẫu hợp kim Nitinol (51%Ti - 49%Ni) có hình dạng thanh, được ép tại nhiệt độ 25°C. Đường cong ứng suất - biến dạng của mẫu tương ứng là đường màu đỏ trên đồ thị (hình 3). Phương trình (2) [26] biểu diễn mối liên hệ giữa ứng suất (σ) với biến dạng (ε), tốc độ biến dạng (ε) và nhiệt độ (T). Các thông số của vật liệu cần thiết cho quá trình mô phỏng được nêu trong bảng 1.
![]()
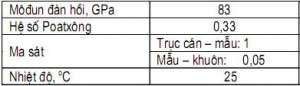
Bảng 1. Các thông số cơ, nhiệt trong mô phỏng số
3. Kết quả và thảo luận
3.1. Góc nghiêng biến dạng
Để xác định góc nghiêng biến dạng của mẫu trong quá trình ép ECAP, J. C. Lee [27] đã tiến hành làm thực nghiệm và xác định được góc nghiêng biến dạng là 43,7°. Trong nghiên cứu này đã mô hình hóa phân tố biến dạng để xác định góc nghiêng của các dải biến dạng bằng phương pháp mô phỏng số. Với thiết lập ban đầu là các phân tố hình vuông trên toàn bộ diện tích của mẫu. Góc nghiêng các dải biến dạng trong kỹ thuật ECAP hay CFAE chính là góc hợp bởi phương trượt với mặt cắt ngang của mẫu.
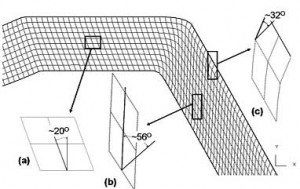
Hình 4. Góc nghiêng biến dạng khi mẫu đi qua các góc kênh sau một lần ép
Trên hình 4 (a), (b) và (c) là kết quả mô phỏng quá trình chuyển dịch và biến dạng các phân tố hình vuông ban đầu. Ta thấy khi mẫu qua góc kênh 150° (hình 4a), phân tố hình vuông bị biến dạng và nghiêng đi một góc α1 = 19,7°. Tiếp đó, mẫu qua góc kênh 120° (hình 4b) góc nghiêng này xác định được là α2 = 56°. Khi mẫu được ép qua góc kênh trong kỹ thuật ECAP các phân tố hình vuông đã bị chuyển hướng đột ngột dẫn tới các cạnh bị xô lệch, có xu hướng kéo dài theo phương trượt và nén lại theo hướng chuyển động của mẫu thành các hình bình hành.
Theo lý thuyết biến dạng dẻo khi các phân tố bị kéo hoặc nén làm các các mặt tinh thể trong các phân tố trượt lên nhau theo các mặt và phương thuận lợi nhất, gây ra sự chuyển dịch tương đối giữa các mặt nguyên tử tạo thành một dải các mặt trượt khi đi qua góc kênh. Quá trình chuyển dịch này được định hướng và phụ thuộc vào yếu tố hình học (góc kênh, Φ) trong kỹ thuật ECAP. Góc nghiêng thể hiện cho mức độ chuyển dịch này càng lớn thì mức biến dạng càng cao.
Ngoài ra, kết quả mô phỏng còn cho thấy, góc nghiêng biến dạng vùng đáy mẫu (hình 4c) α3 (32°) < α2 (56°), điều đó chứng tỏ vùng đáy mẫu biến dạng ít hơn vùng tâm và phía trên của mẫu. Nguyên nhân là do ảnh hưởng của ma sát giữa mẫu và khuôn làm cho biến dạng tại vùng đáy mẫu nhỏ hơn so với vùng phía trên của mẫu.
Kết quả mô phỏng này là góc nghiêng của các dải biến dạng của mẫu sau một lần ép. Nếu tiếp tục ép, các mặt tinh thể trong mẫu chịu các lực cắt, uốn hoặc kéo dài tùy thuộc vào các lộ trình ép khác nhau. Quá trình này tiếp tục tạo ra các dải trượt mới với góc nghiêng biến dạng lớn hơn sau mỗi lần ép.
3.2. Phân bố tốc độ biến dạng
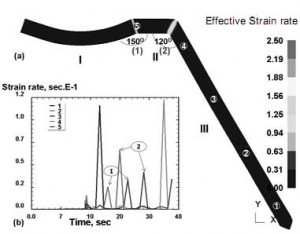
Hình 5. Phân bố và biến thiên tốc độ biến dạng
Hình 5 (a) là phân bố tốc độ biến dạng của mẫu sau khi ép, độ lớn của tốc độ biến dạng được thể hiện bằng màu sắc trên thang đo. Nhận thấy rằng tốc độ biến dạng của mẫu đạt mức cao nhất tại vùng góc kênh 150° (1) và góc kênh 120° (2), nơi xảy ra quá trình trượt mãnh liệt của các mặt tinh thể trong vật liệu và giảm mạnh khi đi qua hai vùng góc kênh này. Để thấy rõ hơn được sự biến thiên của tốc độ biến dạng của mẫu trong quá trình ép đã khảo sát tốc độ biến dạng tại 5 điểm dọc theo chiều dài của mẫu (thể hiện bằng đồ thị trong hình 5 (b)).
Kết quả nhận thấy rằng mỗi điểm (đặc biệt điểm 2 và 3) đều có 3 đỉnh cao nhất ứng với 3 vùng mẫu chịu tác động mạnh nhất, đó là vùng 1 khi trục cán tịnh tiến xuống mẫu. Tại vùng này, giá trị của tốc độ biến dạng đạt được tương đối nhỏ (< 0,2 s-1), vùng 2 là vùng mẫu đi qua góc kênh 150°, tốc độ biến dạng đạt giá trị cao nhất ở vùng này ≈ 0,3 s-1. Tốc độ biến dạng tăng đột ngột và đạt giá trị cực đại ≈ 1,2 s-1 khi mẫu đi qua góc kênh 120° và sau đó giảm mạnh.
3.3. Đánh giá độ đồng đều của mẫu
Độ đồng đều của mẫu sau khi ép qua kênh gấp khúc tiết diện không đổi là một yếu tố quan trọng để đánh giá hiệu quả biến dạng mẫu sau quá trình ép. Mức độ đồng đều có thể xác định bằng sự phân bố biến dạng theo tiết diện mẫu tại các mặt cắt ngang (AB, CD và EF) dọc theo chiều dài mẫu (hình 6).
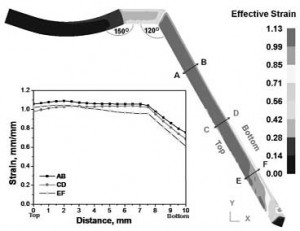
Hình 6. Phân bố biến dạng trên xuống đáy của mẫu tai kênh ra trên 3 mặt cắt AB, CD, EF
Hình 6 mô tả phân bố biến dạng tính từ phía trên của mẫu tại 3 mặt cắt ở các vùng khác nhau của kênh ra. Sự biến dạng của mẫu trên ba mặt cắt AB, CD và EF cao nhất lần lượt là ? 1; 15; 1,05 và 0,95. Trong khoảng 7,5 mm tính từ phía trên của mẫu là khá đồng đều sau đó giảm dần ở phía đáy mẫu. Cũng trên hình 6, nhận thấy ở cả 3 mặt ứng với 3 vùng khác nhau trong mẫu, giá trị biến dạng là khá gần nhau. Như vậy biến dạng của vật liệu trong kỹ thuật CFAE là tương đối đồng đều.
4. Kết luận
Đã xây dựng thành công mô hình 2D kỹ thuật CFAE tương đối cơ bản. Kết quả mô phỏng đã cho thấy góc kênh (Φ) là yếu tố quyết định đến độ lớn của góc nghiêng trên mô hình phân tố biến dạng, góc kênh càng nhỏ thì giá trị góc nghiêng càng lớn. Giá trị góc nghiêng phía trên của mẫu là 56° và phía đáy mẫu là 32° sau một lần ép. Kết quả mô phỏng về phân bố và biến thiên tốc độ biến dạng của mẫu trong quá trình ép, đặc biệt phân tích độ biến dạng qua các mặt cắt ngang AB, CD và EF đã cho thấy biến dạng đồng đều trên mẫu trong kỹ thuật CFAE.
[symple_box color="red" text_align="left" width="100%" float="none"]
LỜI CẢM ƠN
Bài toán mô phỏng thực hiện bởi N.T. Minh và Đ.T.H. Yến tại PTN Công nghệ vật liệu kim loại, Trường ĐHBK Hà Nội. Phần mềm DEFORMTM 2D Ver.9.1 được tài trợ bởi PTN Vật liệu nano (Structural Nano Material Processing Lab.), Trường ĐH POSTECH, Hàn Quốc. [/symple_box][symple_clear_floats][symple_box color="yellow" text_align="left" width="100%" float="none"]
Tài liệu tham khảo và trích dẫn
- J. G. Servilano, P. V. Houtte and A. Aernoudt, Prog. Mater. Sci. 25 (1980) 69-134.
- E. Nes: Prog. Mater. Sci. 41 (1998) 129-193.
- V. M. Segal: Mater. Sci. Eng. A197 (1995) 157-164.
- R. Z. Valiev: Metal Mater. Inter. 7 (2001) 413-420.
- I. V. Alexandrov: Metal Mater. Inter. 7 (2001) 565-571.
- Y. Fukuda, K. Oh-ishi, Z. Horita and T. G. Langdon, Acta Mater. 50 (2002) 1359-1368.
- H. S. Kim, Y. S. Lee, S. I. Hong, A. A. Tarakanova and I. V. Alexandrov, J. Mater. Proc. Technol. 142 (2003) 334-337.
- Y. Saito, H. Utsunimiya, N. Tsuji and T. Sakai, Acta Mater. 47 (1999) 579-583.
- A. Belyakov, T. Sakai, H. Miura and R. Kaibyshev: Phil. Mag. Lett. 80 (2000) 711-718.
- H. S. Kim: Mater. Sci. Eng. A, 32-8 (2002) 317-323.
- Y. Beygelzimer, V. Varyukhin, D. Orlov, S. Synkov, A. Spuskanyuk, Y. Pashinska, M. J. Zehetbauer, R. Z. Valiev, Germany, Wiley–VCH Verlag (2004) 511.
- S. C. Yoon, S. J. Hong, M. H. Seo, P. Quang and H. S. Kim, Journal of Korean Powder Metallurgy Institute, 11(2) (2004) 87-94.
- P. Quang, Y. G. Jeong, S. H. Hong and H. S. Kim, Key Eng. Materials Vols. 326-328 (2006) 325-328.
- P. Quang, Y. G. Jeong, S. C. Yoon, S. I. Hong, S. H. Hong and H. S. Kim, Materials Science Forum Vols. 534-536 (2007) 245-248.
- P. Quang, Y. G. Jeong, S. C. Yoon, S. H. Hong and H. S. Kim, Journal of Materials Processing Tech., Vols. 187-188 (2007) 46-50
- Y. Iwahashi, J. Wang, Z. Horita, M. Nemoto and T. G. Langdon, Scripta Mater. 35 (1996) 143-146.
- Phạm Quang, Phùng Trí Điểm, Nguyễn Thị Huyền, Nguyễn Thị Hoàng Oanh, Đỗ Minh Nghiệp và Yong Jin Kim, Kỷ yếu Hội nghị khoa học và công nghệ lần thứ 11- HCMHUT, vol. 0701(2009) 2217-2223.
- D. V. Hai, D. M. Ngung, D. M. Nghiep and N.T. Giang, Proceeding: Advanced Technologies for Materials Production and Processing, Viện HLKH Belarus (2010) 41-46.
- P. Quang, D. M. Nghiep and Y. J. Kim, Proceeding: Advanced Technologies for Materials Production and Processing, Viện HLKH Belarus (2010) 28-35.
- G. J. Raab, R. Z. Valiev, T. C. Lowe, Y. T. Zhu, Mater. Sci.Eng. A382(200 4)30.
- J. W. Park, J. W. Kim and Y. H. Chung, Scripta Mater. 51 (2004) 181.
- J. Y. Suh, J. H. Han, K. H. Oh and J. C. Lee, Scripta Mater. 49 (2003) 185.
- Y. Huang and P. B. Prangnell, Scripta Mater. 56 (2007) 333-336.
- DEFORMTM 2D V9.1 Software, Scientific Forming Technologies Corporation.
- E. A. Brandes, Smithells metals reference book, Butterworths, 1983.
- DEFORMTM 2D V9.1 User manual, Scientific Forming Tech. Corporation, Columbus, Ohio, 43220.
- J. C. Lee, H. K. Seok and J. Y. Sub, Acta Mater. 50 (2002) 4005-4019.
[/symple_box][symple_clear_floats]